パラメトリック図の作成

ここでは、シミュレーションのためのSysMLモデルの作成方法について説明します。作成後には、SysMLシミュレーションの設定タブから作成したモデルの設定を行い、シミュレーションを実行して結果を表示します。ポイントになる点について、画像を含めて説明します。

パラメトリック図を作成する際に、等式制約を指定する方法として次の3つの方法があります。

ブロック内に制約として定義する
制約ブロック要素を定義し利用する
制約プロパティを接続して定義する

また、以下の点について考慮する必要があります。

物理的なやりとりの流れ
既定値と初期値
シミュレーション関数
値の割り当て
パッケージとインポート

等式制約

ブロック内の等式制約

等式制約を定義する最も簡単な方法は、ブロックに制約を定義する方法です。

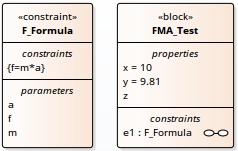
次の図では、等式" f = m * a "が制約としてブロック内に定義されています。

上記の要素を例に、1つのブロックに複数の等式制約を定義できます。

#	説明
1	SysMLシミュレーションの設定要素"Force=Mass*Acceleration(1)"を定義し、要素"FMA_Test"が含まれるパッケージを対象として指定します。
2	"FMA_Test"をSysMLSimModelとして設定します。
3	パートプロパティ "a" と "m" をSimConstantに設定し、パートプロパティ "f" をSimVariableに設定します。
4	"f"を対象にプロットし、シミュレーションを実行します。
5	解析ボタンを押し、結果を表示します。

結果として、チャートからf = 98.1 (10 * 9.81)を導くことができます。

制約プロパティの接続

SysMLでは、制約ブロック内の制約プロパティを、より柔軟な方法で利用して制約を定義できます。

次の図では、制約ブロックKはパラメータa,b,c,d,KValの5つのパラメータと、eq1,eq2,eq3の3つの制約プロパティを持ちます。制約プロパティは、それぞれK1,K2,K1MultiplyK2の型に設定されています。

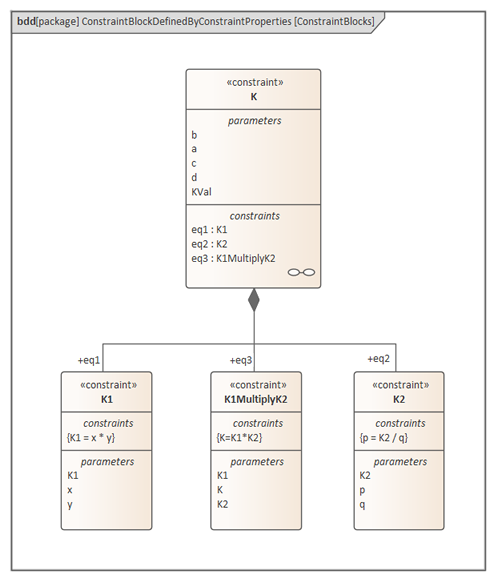
制約ブロックK内にパラメトリック図を作成し、パラメータと制約を束縛コネクタで結びます。

5つのプロパティを持つMyBlockを定義します。
制約プロパティeqを作成し、パラメータを表示します。
プロパティとパラメータを束縛コネクタで結びます。

データセットで、(arg_a = 2, arg_b = 3, arg_c = 4, arg_d = 5) の値を設定します。
シミュレーションの設定で、MyBlock, DataSet_1を対象とします。
プロット対象として 'arg_K' にチェックを入れます。
シミュレーションを実行します。

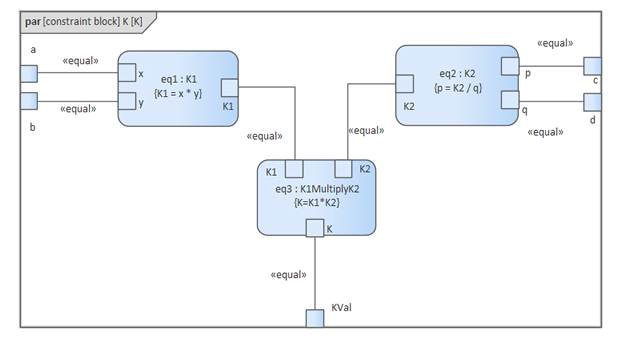
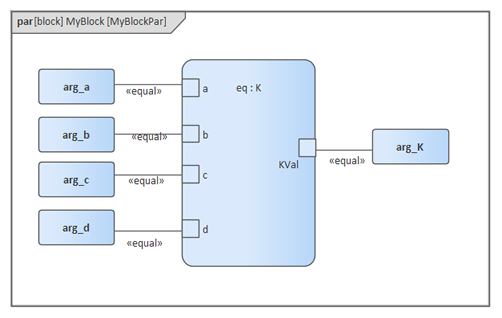
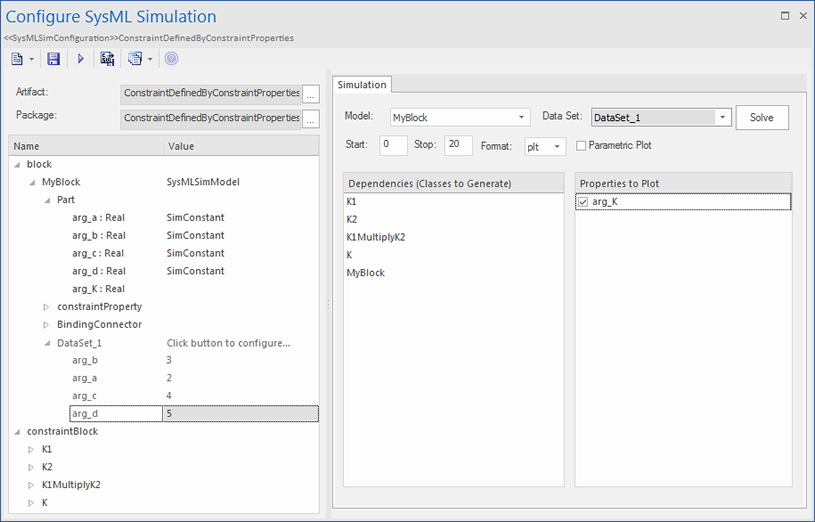
結果は120 (2 * 3 * 4 * 5)となります。これは、K = K1 * K2 = (x*y) * (p*q) という式があり、それに対して実際の値を割り当てて (2 * 3) * (4 * 5)　という計算になっています。

ここで、K2に関する等式(制約)を"p = K2 / q"と変更しても、このサンプルは正しく動作します。このように、後から制約を変更できます。

今回の例では、"K2"が"p * q"という簡単な制約でしたのでこうしたシミュレーションを利用しなくても簡単に解を得ることができます。しかし、実際には複雑な制約・等式になると、こうしたシミュレーション機能を利用して解を導く方が効率的です。

このように、制約ブロックや制約プロパティを定義して等式を定義できます。このような制約ブロックと制約プロパティの関係は、階層化される場合でも利用できます。つまり、制約プロパティを利用して定義した制約ブロックを、さらに制約プロパティとして別の制約ブロックの定義に利用できます。

再利用可能な制約ブロックを作成する

特定の等式が複数のブロックで利用される場合には、制約ブロックを、複数のブロックのプロパティとして利用できるように定義できます。今までの例を元に修正します。

　制約ブロック要素 'F_Formula' を定義し、3つのパラメータ 'a', 'm', 'f'' と、制約 'f = m * a' を定義します。

注意:

プロパティの型を指定していない場合には、プリミティブ型Realが適用されます。

ブロック 'FMA_Test' を定義し、3つのプロパティ 'x', 'y', 'z' を追加します。 'x' と 'y' の初期値として '10' と '9.81'　を指定します。
'FMA_Test' の子ダイアグラムとしてパラメトリック図を作成します。,プロパティ 'x', 'y', 'z' が表示されます。
制約プロパティ 'e1' を作成します。型は 'F_Formula' です。関係するパラメータを図に表示します。
下の図のように、それぞれを結びます。

SysMLSimConfiguration 成果物要素を作成し、以下のように設定します。

'FMA_Test' の 'Value' の列には、'SysMLSimModel' を指定します。
'x' と 'y' の 'Value' の列には、 'SimConstant'を指定します。
'プロットするプロパティ' では、 'Z' にチェックを入れます。
解析ボタンを押し、シミュレーションを実行します。

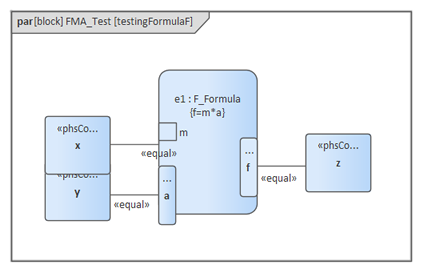
結果のグラフから f = 98.1 (10 * 9.81 の結果) とわかります。

物理的なやりとりの流れ

物理的なやりとりのモデリングを行う場合には、物理的な物体の交換をフローとしてモデリングし、属性"isConserved"をフローの変数として定義する必要があります。こうした例は、例えば電圧・力・トルクなどがあります。

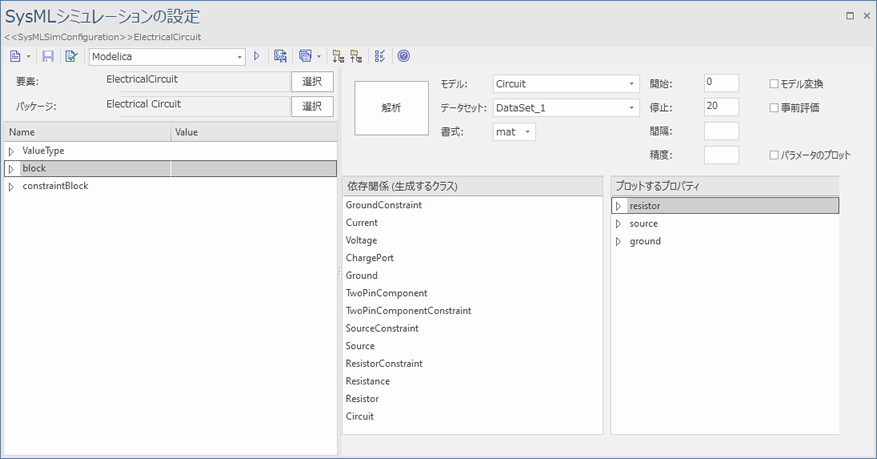
次の例は、"ElectricalCircuit"のサンプルにおける生成されたコードの例です。

connector ChargePort

flow Current i; //flow keyword will be generated if isConserved = true

Voltage v;

end ChargePort;

model Circuit

Source source;

Resistor resistor;

Ground ground;

equation

connect(source.p, resistor.n);

connect(ground.p, source.n);

connect(resistor.p, source.n);

end Circuit;

それぞれのconnectの等価式は、以下のような2つの式に展開されます。1つは等価を示す式で、もう1つは合計値がゼロになる関係を示しています。

source.p.v = resistor.n.v;

source.p.i + resistor.n.i = 0;

既定値と初期値

もし、SysMLのモデルで初期値(プロパティサブウィンドウの「プロパティ」タブ内の初期値の欄)が設定されている場合には、その値がシミュレーションの既定値としても利用されます。SimConstantの場合はその値が固定値となり、SimConstantは初期値となります。

次の振り子のモデルの例では、プロパティg, L, m, PI x, yに初期値を設定しています。このうち、PI(円周率), m (振り子の質量), g (重力定数), L(振り子の長さ)はシミュレーション中に変化しませんので、SimConstantとして定義されています。

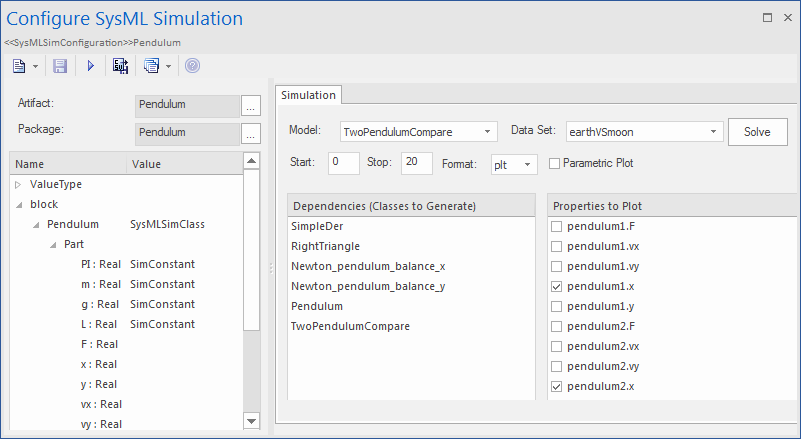
生成されるコードは次のようになります。

class Pendulum

parameter Real PI = 3.141;

parameter Real m = 1;

parameter Real g = 9.81;

parameter Real L = 0.5;

Real F;

Real x (start=0.5);

Real y (start=0);

Real vx;

Real vy;

......

equation

......

end Pendulum;

プロパティ PI, m, g, L は定数として定義されています。
プロパティ x, yは変数なので、初期値として 0.5と0が設定されています。

シミュレーション関数

関数は、制約内で利用できる機能で、複雑なロジックを簡単に利用するための方法です。

次の例では、貯水タンクの例で利用されている関数です。

制約ブロック"Q_OutFlow"では、関数"LimitValue"が定義・利用されています。

ブロックや制約ブロックに対して操作を作成し、その操作のプロパティを開きます。
操作のステレオタイプとして"SimFunction"を指定します。
引数と入出力の向きを指定します。

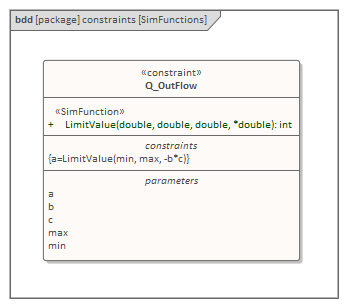
なお、複数のパラメータを出力として定義できます。

(out1, out2, out3) = function_name(in1, in2, in3, in4, ...); //Equation form

(out1, out2, out3) := function_name(in1, in2, in3, in4, ...); //Statement form

関数の本体は、振る舞いタブ内の"既定のソースコード"として記載します。

この例における本体の内容は次の通りです。OpenModelicaで解釈できる内容で記載します。

pLim :=

if p > pMax then

pMax

else if p< pMin then

pMin

else

ソースコード生成を実行すると、ブロックや制約ブロックが持つSimFunctionのステレオタイプが設定された操作を探索し、ソースコードに出力します。

function LimitValue

input Real pMin;

input Real pMax;

input Real p;

output Real pLim;

algorithm

pLim :=

if p > pMax then

pMax

else if p< pMin then

pMin

else

end LimitValue;

値の割り当て

次の例は、"Force=Mass*Accelaration".を示すシンプルなモデルの例です。

ブロック"FMA"はプロパティa, f, mと、制約プロパティe1を持ちます。e1の型は"F_Fomular".です。
ブロック"FMA"のプロパティには初期値の設定はありません。シミュレーション時に設定し、内容が変化する変数という想定です。
ブロック"FMA_Test"をSysMLSimModelとして定義し、ブロック"FMA"を型とするプロパティfma1を追加します。
制約として、a_valueの値をsin(time)とします。
制約として、m_valueの値をcos(time)とします。
Allocationの接続を"FMA"のモデル内で利用し、値を割り当てます。

プロットするプロパティとして 'fma1.a', 'fma1.m', 'fma1.f' にチェックを入れてください。
「解析」ボタンを押し、シミュレーションを実行します。

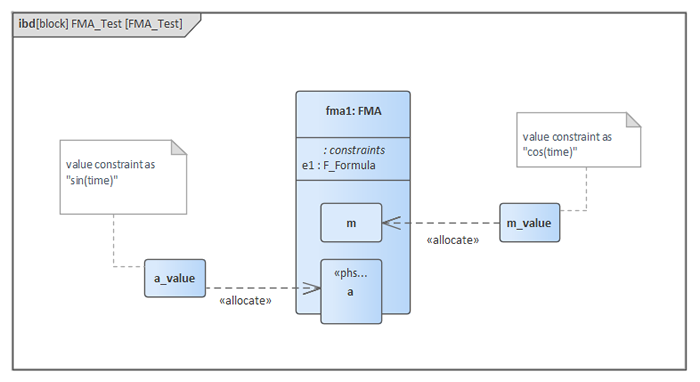
シミュレーションの結果は次の通りです。

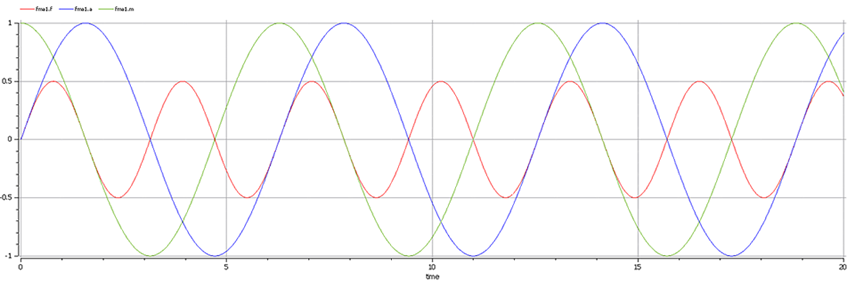
パッケージとインポート

SysMLシミュレーションの設定要素では、対象とするパッケージ内の、シミュレーションに関係する要素の情報を収集します。もし、シミュレーションのモデルが、対象のパッケージに含まれていない要素に依存している場合には、シミュレーションで利用するためにパッケージ間にインポートの関係を定義する必要があります。

電気回路の例では、シミュレーション対象のパッケージは"ElectricalCircuit"です。このパッケージ内にシミュレーションに関係する要素のほぼすべてが含まれていますが、いくつかのプロパティの型は別のパッケージ"CommonlyUsedTypes"で定義されています。このような場合には、パッケージ間にインポートの関係を作成することで、関係する要素をすべてシミュレーションの対象として含めることができます。

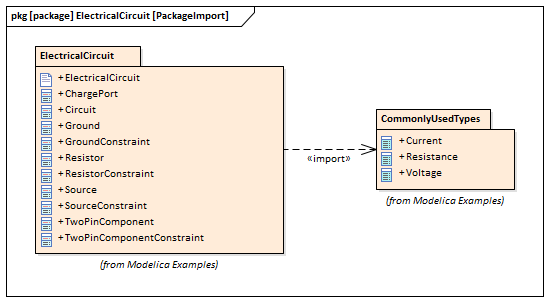
参照:

OpenModelicaとの連携